Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is

Question

Philoid · Accepted Answer

Given: A deck of cards.

X be the number of aces obtained.

Hence, X can take value of 0, 1 or 2.

As we know, in a deck of 52 cards, 4 cards are aces. Therefore 48 cards are non- ace cards.

P(X = 0) = P(0 ace and 2 non ace cards)

P(X = 1) = P(1 ace and 1 non ace cards)

P(X = 2) = = P(2 ace and 0 non ace cards)

Hence, the required probability distribution is,

X	0	1	2
P(X)

Therefore Expectation of X E(X):

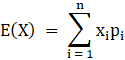
Hence, the correct answer is (D).