An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that:
(i) All will bear 'X' mark.
(ii) Not more than 2 will bear 'Y' mark.
(iii) At least one ball will bear 'Y' mark.
(iv) The number of balls with 'X' mark and 'Y' mark will be equal.
(i) It is given in the question that,
Total number of balls in the urn = 25
Number of balls bearing mark ‘X’ = 10
Number of balls bearing mark ‘Y’ = 15
Let p denotes the probability of balls bearing mark ‘X’ and q denotes the probability of balls bearing mark ‘Y’
∴ ![]()
And, ![]()
Now, 6 balls are drawn with replacement. Hence, the number of trials are Bernoulli triangle.
Let us assume, Z be the random variable that represents the number of balls bearing ‘Y’ mark in the trials
∴ Z has a binomial distribution where n = 6 and ![]()
![]()
Hence, P (All balls will bear mark ‘X’) = P (Z = 0)
![]()
![]()
(ii) Probability (Not more than 2 will bear ‘Y’ mark) ![]()
= P (Z = 0) + P (Z = 1) + P (Z = 2)
![]()
![]()
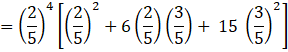
![]()
= ![]()
(iii) Now, Probability (At least one ball will bear ‘Y’ mark) = P (Z ≥ 1)
= 1 – P (Z = 0)
= ![]()
(iv) Probability (Having equal number of balls with ‘X’ mark and ‘Y’ mark) = P (Z = 3)
![]()
= ![]()
= ![]()