Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decay in the decay scheme shown in Fig. 13.6. You are given that
m(198Au) = 197.968233 u
m(198Hg) = 197.966760 u
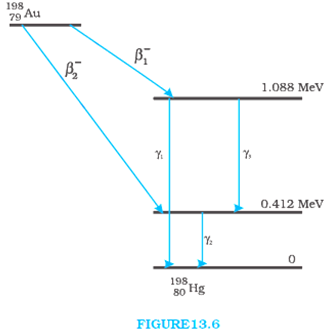
From the given diagram γ1 decays from the 1.088 MeV energy level to 0 MeV level.
We have,
E = hν
Where,
h = plank’s constant = 6.6×10-34 J s
ν = frequency
Thus, frequency of radiation radiated by γ1 decay is given by,
(∵ 1 eV = 1.6×10-19 C )
Thus, frequency of radiation radiated by γ2 decay is given by,
(∵ 1 eV = 1.6×10-19 C )
Thus, frequency of radiation radiated by γ3 decay is given by,
(∵ 1 eV = 1.6×10-19 C )
Given,
Mass of 
, m1 = 2.014102 u
Mass of 
, m2 = 3.016049 u
The energy of the highest level is given by,
Where,
Δm = Mass defect (or) mass lost during reaction
c = speed of light
∴ E = (197.968233 – 197.966760) u×c2
= 0.001473 u×931.5 MeV/c2
= 1.3720995 MeV
Since, β1 decays from maximum level to 1.088 MeV level then,
Kinetic energy of the β1 particle = (1.3720995 – 1.088) MeV
= 0.2840995 MeV
Since, β2 decays from maximum level to 0.412 MeV level then,
Kinetic energy of the β2 particle = (1.3720995 – 0.412) MeV
= 0.9600995 MeV