Evaluate 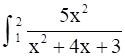
Let I = 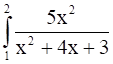
Dividing 5x2 by x2 + 4x + 3 we get 5 as quotient and –(20x + 15) as remainder
So, I = 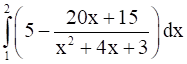
⇒ I = 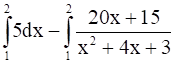 =
= 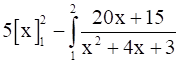
⇒ I = 5 (2 – 1) - 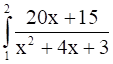
⇒ I = 5 – I1
I1 = 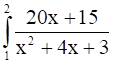
Adding and subtracting 25 in the numerator
I1 = 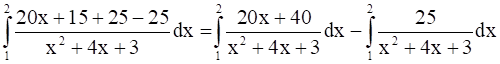
I1 = 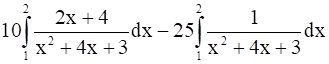
Let x2 + 4x + 3 = t
(2x + 4)dx = dt
∴ I1 = 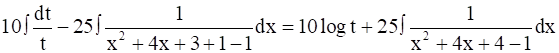
I1 = 10 log t - 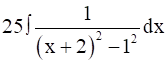 [
[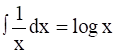 ]
]
I1 = 10 log t - 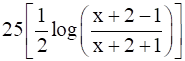 [
[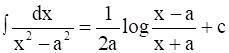 ]
]
I1 = 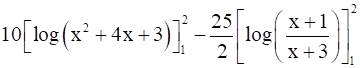
I1 = 10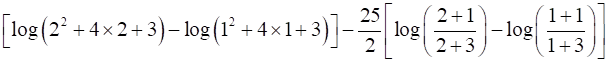
I1 = 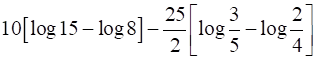
I1 = 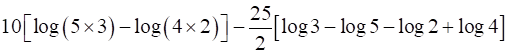
I1 = 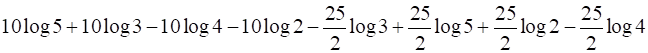
I1 = 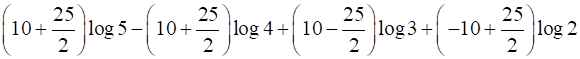
I1 = 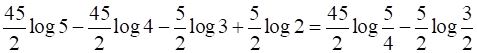
∵ I = 5 – I1
Substituting I1 in I we get
I = 5 – 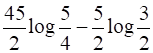
∴ 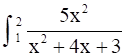 = 5 –
= 5 – 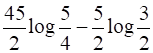
19