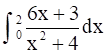
Let I =

I =

∴ I = I₁ + I₂

I₁ =

Let x² + 4 = t

2x dx = dt

When x = 0; t = 4

When x = 2; t = 2² + 4 = 8

Substituting t and dt in I₁

⇒ I₁ = []

⇒ I₁ = 3 [log |8| - log |4|] = 3 log 8/4

⇒ I₁ = 3 log � = -3 log 2

I₂ = = []

⇒ I₂ =

⇒ I₂ = = 3π/8

Now I = I₁ + I₂

I = 3 log � + 3π/8

∴ = 3 log � + 3π/8