Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are externally in the ratio 1 : 2. Also, show that P is the midpoint of the line segment RQ.

Question

Philoid · Accepted Answer

Given: points are given.

Point R is given which divides P and Q in the ratio 1:2.

Then

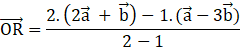
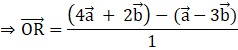
∴ position vector of R is

And position vector of mid-point of RQ =

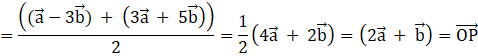
Hence, P is mid-point of the line segment RQ.