A physical quantity P is related to four observables a, b, c and d as follows:
![]()
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?
Given:
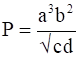
The percentage error in a i.e. 
The percentage error in b i.e. 
The percentage error in c i.e. 
The percentage error in d i.e. 

(Rule: The relative error in a
physical quantity raised to the power k is the
k times the relative error in the individual
quantity- given in NCERT class 11-chapter 2 page 27)
Multiplying both sides by 100 will make each quantity % and thus we can directly substitute the given values to find ΔP/P % or percentage error in P.
ΔP/P % = 3×1 + 2× 3 + 0.5× 4 + 2 = 13 %
Since number of significant digits in ΔP/P are 2, P should also have 2 significant digits.
P = 3.8 (rounded off to first decimal place)