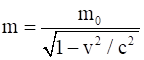A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ mo of a particle in terms of its speed v and the speed of light, c. (This relation first arose as a consequence of special relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes:

Guess where to put the missing c.
The dimension of the quantities involved are:
m = M1L0T0
m0 = M1L0T0
v = M0L1T-1
c = M0L1T-1
For a correct dimensional equation, the dimensions of LHS and RHS should be equal. We can see that dimensions of m and m0 are equal thus the remaining part of the equation should be constant.
 should be unitless.
should be unitless.
1 is dimensionless so ![]() should be dimensionless.
should be dimensionless.
On subtraction, dimension of the 2 quantities should be same. So, dimension of 1 and v2 should be same. Therefore, v2 should be dimensionless and therefore v.
We can see that dimension of v and c are same. So, replacing v by v/c will make it dimensionless and the given equation dimensionally correct.
Hence, correct relation will be,