In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?
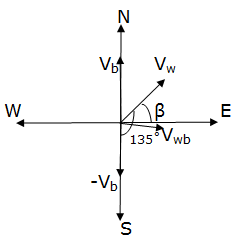
Figure showing velocity of wind and the boat
Given:
Velocity of wind = Vw = 72 km/hr along N-E direction
Velocity of boat = Vb = 51 km/hr along N direction
Explanation: To find out the direction of flag on the mast of the boat, we need to find out the relative velocity of wind w.r.t the boat.
Relative velocity of wind w.r.t the boat = Vwb = Vw - Vb
= 72 - Vb
Angle between Vw and -Vb = 135˚
Using parallelogram law of vectors, let Vwb be the resultant vector making an angle β with Vw
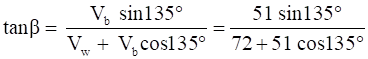
= 1.0034
β = 45.099˚
= 4.1˚ w.r.t N-E direction
i.e. 45.1˚-45˚ = 0.1˚ w.r.t East
The direction of flag on the mast of the boat is 0.1˚ w.r.t East.