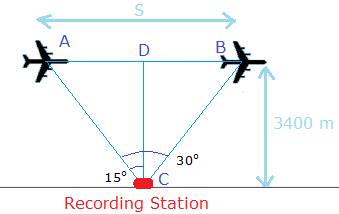
now let the aircraft be initially at a point A situated 3400m above the ground, it moves with a speed v along straight line parallel to ground and reach a point B, now let us assume a recording station is located on ground at c which is in line with midway of the journey D

Suppose the plane covered a distance S and subtended an angle of 30^o on recording station as it moved from A to B

The situation has been shown in the figure

We have to find speed of the plane; the plane is moving with constant speed so we will use the relation

S = v × t or v = S/t

Where S is the distance covered by plane moving with a speed v in time t

Here we are given time t = 10.0 s

So we need to find distance covered by plane S

Now we can see distance covered = AB = AD + BD

Since D is the midpoint of AB

AD = BD or distance AB = 2 × AD

Now in Triangle ACD using trigonometry we will find AD

now

Assuming D is the midpoint of AB and C is equidistant from A and B we have

Or

AD = CD × tan15^o

CD = 3400m

tan15^o= 0.2679

so we get

AD = 3400m × 0.2679

= 910.86m

So total distance covered by the plane

S = AB = 2 × 910.86m = 182.17m

So the Value of S = 182.17m and t = 10 s in the equation

v = s/t ,we get

speed of the plane

so plane is flying at a speed of 18.2 m/s