A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?
A vector quantity is one which has both magnitude and direction but should also obey laws of vector addition subtraction and multiplication for e.g. Electric Current has both magnitude and direction but is not a vector it is added algebraically not vectorially so it is a scalar quantity suppose current I1 and I2 are flowing as shown in figure both have same magnitude the net current is I = I1 + I2 = 2 I1 = 2I2
If if we would have added them using vector laws, both are equal in magnitude and opposite in direction so resultant would have been zero which is incorrect so current is not vector
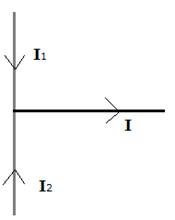
likewise, all quantities having both magnitude and direction are not vectors
Now suppose a body is rotating about a fixed axis and has rotated by an angle