Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and pz. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
From the given data,
Linear momentum vector, ![]()
Position vector, ![]()
We have, Angular momentum, ![]()
= ![]()
= 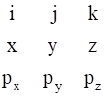
∴ ![]()
By comparing respective components, we get,
![]()
![]()
![]()
Since, the particle moves in x-y plane, then the ![]() vectors of both position and linear momentum vectors be Zero.
vectors of both position and linear momentum vectors be Zero.
Thus,
![]()
![]()
![]()
Hence, the particle moves in x-y plane the angular momentum acts towards z-direction.
8