A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10 π rad/s. Which of the two will start to roll earlier? The co-efficient of kinetic friction is μk= 0.2.
Given,
Radius of the disc and ring, r = 10 cm = 0.1 m
Angular velocity of the disc and ring, ω0 = 10 π rad/s
Initial velocity of both the objects, u = 0 m/s
Coefficient of kinetic friction, μk = 0.2
Motion of the objects start due to frictional force,
f = ma
Where f = frictional force ,
⇒ f = μkmg
m = mass of the body
a = acceleration of the body
∴ μkmg = ma
⇒ a = μkg ------ > (1)
We have final velocity as per first equation of motion,
v = u + at
Where,
v = final velocity
u = initial velocity
a = acceleration
t = time
∴ v = μkg ------- > (2)
The torque generated by friction initially causes reduction in angular velocity. Thus,
T = -Iα
Where,
I = moment of inertia of the body
α = Angular acceleration
and, T = fr
Where,
f = frictional force
r = radius
∴ T = -μkmgr
⇒  ------- > (3)
------- > (3)
As per the frist equation of rotational motion, final angular velocity,
ω = ω0 + αt
Where,
ω0 = intial angular velocity
α = angular acceleration
t = time
∴  ------ > (4)
------ > (4)
Rolling starts when linear velocity, v = rω
∴  -------- > (5)
-------- > (5)
From the equations 2 & 5 we get,
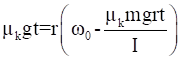
⇒  ------- > (6)
------- > (6)
We know that,
For the ring, I = mr2
∴ 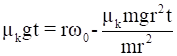
⇒ μkgt = rω0 – μkgt
⇒ 2μkgt = rω0
∴ 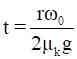
⇒ tring
⇒ tring = 0.8s
For the disc, I = 0.5mr2
∴ 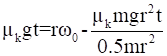
⇒ ![]()
⇒ 3μkgt = rω0
∴ 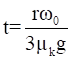
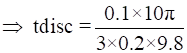
⇒ tdisc ![]()
Since the tdisc < tring.
Therefore, the disc will start rolling before the ring.