A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 300. The coefficient of static friction μs = 0.25.
A. How much is the force of friction acting on the cylinder?
B. What is the work done against friction during rolling?
C. If the inclination q of the plane is increased, at what value of q does the cylinder begin to skid, and not roll perfectly?
Given,
Mass of the cylinder, m = 10 kg
Radius of the cylinder, r = 15 cm = 0.15 m
Inclination angle, θ = 300
Coefficient of static friction, μs = 0.25
The moment of inertia of the cylinder about its geometric axis is given by, I = 0.5mr2
The free diagram of the body is given by,
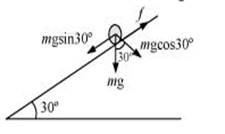
We have,
A. From the newton second law of motion, force net,
Fnet = ma
Where,
m = mass of the body
a = acceleration of the body
∴ mg sinθ – f = ma
⇒ f = ma – mg sinθ
= (10×3.27)-(10×9.81×sin30)
= 16.3 N
B. During rolling the instantaneous point of contact have zero velocity. Thus, work done against frictional force is zero.
C. For rolling without skid, we have,
⇒ 3μ = tan θ