(a) Now here when springs are stretched by a force F they will apply a restoring force in opposite direction when extension in length of spring is there as the extension in the spring increases the restoring force in the spring also increases so there are two Forces acting on each block in opposite direction when external applied force is equal to the restoring force of the block the block will be in equilibrium the free body diagram for block in fig (a)

has been shown in the figure below

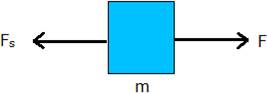
Restoring Force of spring F_s is acting in left direction and is equal in magnitude to applied force acting in right direction i.e. F = F_s

We know restoring force in a spring is given as

F_s = Kx

Where K is the spring constant of the spring and x ia the extension in the spring

So we have

F = Kx

i.e. x = F/K

or the extension in length of spring is

x = F/K

now in case (b) the spring is holding two blocks in equilibrium as spring always applies restoring force in a direction opposite to the direction of applied force, so for Block A on left external force is to the left so spring force will be in right direction and will be equal in magnitude to the external force and for Block B on Right external force is to the Right so spring force will be in Left direction and will be equal in magnitude to the external force, the free body diagram of both the blocks has been

shown in the figure

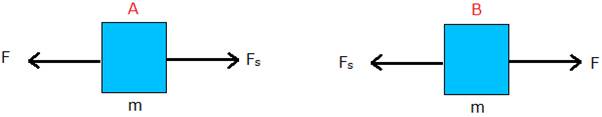
So we have

F = F_s (For Both the blocks)

We know restoring force in a spring is given as

F_s = Kx

Where K is the spring constant of the spring and x is the extension in the spring

So we have

F = Kx

i.e. x = F/K

or the extension in the length of spring is

x = F/K

(b) When the mass in (a) is releases it will start oscillating and perform simple harmonic motion since for we know condition for simple harmonic motion is that acceleration of particle is proportional to distance from mean position and is directed toward mean position

and we have relation between acceleration and displacement as

a = -ω²x

where a is the acceleration of particle undergoing Simple Harmonic Motion with angular frequency ω and x is the displacement from mean position

here on the block of mass m, when it is at a distance x from original position or mean position

force is

F = -Kx (Force is in opposite direction to displacement )

Where K is Spring constant

Now we know

F = ma

Where F is the force acting on a body of mass m whose acceleration is a

So we have

ma = -Kx

or the acceleration of the mass is

a = -(K/m)x

since spring constant K and mass of block m are constant quantities so we can say acceleration of block is proportional to displacement from mean position and we know it is directed towards mean position so block is executing simple harmonic motion so comparing with equation of simple harmonic motion we get

ω²= K/m

where ω is the angular frequency of simple harmonic motion

now we get

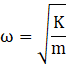
We know relation between time period T and angular frequency ω as

T = 2π/ω

So we have the time period of the oscillation as

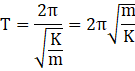
So the time period of simple harmonic oscillation is

Where m is the mass of the block and K is the spring constant

Now in Case (b) again both blocks will move to and fro from each other and start oscillating simple harmonically and the mean position will be different for both blocks on either side of centre of spring

As shown in the figure

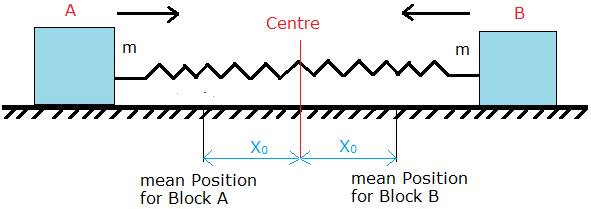
Now the spring can be divided in two parts and we can x₀ is the natural length of both part of spring on either side, now considering any one Block we can say time period of oscillation is

Where m is the mass of the block and K’ is the spring constant for that part

When a spring is cut to half value of spring constant doubles

So if K is the original spring constant, Spring constant of each part is

K’ = 2K

So time period is

Where m is mass of each block and K is the spring constant of the spring.