The acceleration due to gravity on the surface of moon is 1.7 m s–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 m s–2)
Time Period of a simple pendulum is time taken by pendulum to complete one complete oscillation, we know time period of a simple pendulum is given by the relation
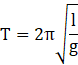
Where T is the time period of the Simple Pendulum
l is the length of the pendulum, having a bob of mass m and g is the acceleration due to gravity
A simple Pendulum is shown in the figure

Let the time period of simple pendulum on earth be
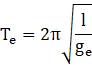
Where Te is the time period of the Simple Pendulum on earth
l is the length of the pendulum, and ge is the acceleration due to gravity on earth
And let the time period of pendulum on moon be

Where Tm is the time period of the Simple Pendulum on Moon
l is the length of the pendulum, and gm is the acceleration due to gravity on Moon
diving both equations we get
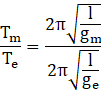
Solving and cancelling terms we get

Or we can say Time period of simple pendulum on moon is
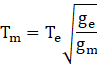
Where Time period of simple pendulum on moon is
Te = 3.5 s
Acceleration due to gravity on moon is
gm = 1.7 m s–2
Acceleration due to gravity on earth is
ge = 9.8 m s–2
so putting these value we get Time period of simple pendulum on moon is

![]()
So time period of the simple pendulum on moon is 8.40 s