A point R with x-coordinate 4 lies on the line segment joining the points P(2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.
[Hint Suppose R divides PQ in the ratio k : 1. The coordinates of the point R are given by

Given: The coordinates of the points P (2, -3, 4) and Q (8, 0, 10).
⇒ x1 = 2, y1 = -3, z1 = 4; x2 = 8, y2 = 0, z2 = 10
Let the coordinates of the required point be (4, y, z).
Now, let the point R (4, y, z) divides the line segment joining the points P (2, -3, 4) and Q (8, 0, 10) in the ratio k : 1.
Also, by Section Formula,
We know that the coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m : n is given by:
![]()
So, the coordinates of the point R are given by ![]()
So, we have ![]()
![]()
⇒ 8k + 2 = 4 (k + 1)
⇒ 8k + 2 = 4k + 4
⇒ 8k – 4k = 4 – 2
⇒ 4k = 2
![]()
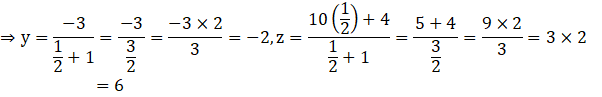
Hence, the coordinates of the required point are (4, -2, 6).