The n^th term of series is

Now, first solve the numerator & denominator separately

1³ + 2³ + 3³ + … + n³ …(1)

Also,

1 + 3 + 5 + … + n terms

This is an AP.

whose first term(a) =1 & common difference(d) = 3 - 1 = 2

Now, sum of n terms of AP is

S_n = (n/2)[2a + (n - 1)d]

= (n/2)[2(1) + (n - 1)2]

= (n/2)[2 + 2n - 2]

= (n/2)[2n]

= n²

∴ S_n = n² …(2)

Now,

putting values from (1) & (2)

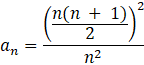
Now, Finding Sum of n terms of Series

Thus, the required sum is