The origin of the coordinate plane is taken at the vertex of the parabolic reflector in such a way that the axis of the reflector is along the positive x – axis.

This can be diagrammatically represented as

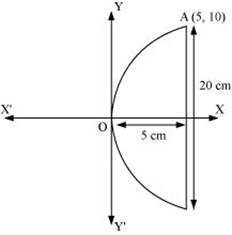
The equation of the parabola is of the form y² = 4ax (as it is opening to the right)

Since, the parabola passes through point A(10, 5), 10² = 4a(5)

⇒ 100 = 20a

⇒ a = = 5

Therefore, the focus of the parabola is (a, 0) = (5,0), which is the mid – point of the diameter.

Hence, the focus of the reflector is at the mid-point of the diameter.