An equilateral triangle is inscribed in the parabola y 2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.

Question

Philoid · Accepted Answer

Let OAB be the equilateral triangle inscribed in parabola y² = 4ax.

Let AB intersect the x – axis at point C.

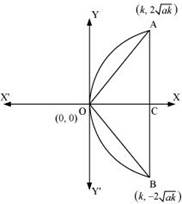
Let OC = k

From the equation of the given parabola, we have,

y² = 4ak

⇒ y = 2

Thus, the respective coordinates of points A and B are (k, 2 ), and (k, -2)

AB = CA + CB = 2

Since, OAB is an equilateral triangle, OA² = AB².

Thus,

⇒ k² + 4ak = 16ak

⇒ k² = 12ak

⇒ k = 12a

Thus, AB =

Thus, the side of the equilateral triangle inscribed in parabola y² = 4ax is .

An equilateral triangle is inscribed in the parabola y2 = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.

An equilateral triangle is inscribed in the parabola y² = 4 ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle.