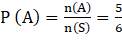A die is thrown; find the probability of following events:
(i) A prime number will appear,
(ii) A number greater than or equal to 3 will appear,
(iii) A number less than or equal to one will appear,
(iv) A number more than 6 will appear,
(v) A number less than 6 will appear.
Here S = {1, 2, 3, 4, 5, 6}
∴n(S) = 6
(i) Let A be the event of getting a prime number,
A = {2, 3, 5} and n(A) = 3
![]()
(ii) Let A be the event of getting a number greater than or equal to 3,
Then A = (3, 4, 5, 6) and n(A) = 3
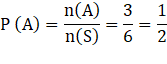
(iii) Let A be the event of getting a number less than or equal to 1,
Then A = (1) ∴ n (A) = 1
![]()
(iv) Let A be the event of getting a number more than 6, then
Then A = (0), ∴ n (A) = 0
![]()
(v) Let A be the event of getting a number less than 6, then
Then A= (1, 2, 3, 4, 5), ∴ n (A) = 5