To prove cot4x (sin5x + sin3x) = cot x (sin5x – sin3x)

LHS = cot 4x (sin 5x + sin 3x)

We know,

LHS = cot 4x × 2 sin 4x × cos x

LHS = 2 cos 4x cos x

RHS = cot x (sin 5x – sin 3x)

We know,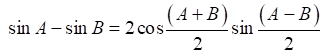

RHS = cot x × 2 cos 4x × sin x

RHS = 2 cos 4x cos x

∴ LHS = RHS

Hence, proved