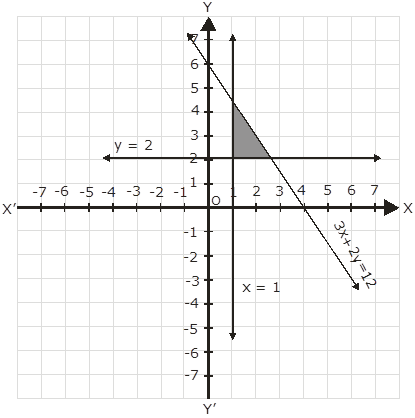
Solve the following system of inequalities graphically:
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Given 3x+ 2y ≤ 12
Solving for the value of x and y by putting x = 0 and y = 0 one by one
We get
y = 6 and x = 4
So the points are (0,6) and (4,0)
Now checking for (0,0)
0 ≤ 12 which is also true,
Hence the origin lies in the plane and the required area is toward the left of the equation.
Now checking for x ≥ 1,
The value of x would be unaffected by any value of y
The origin would not lie on the plane
⇒ 0 ≥ 1 which is not true
The required area to be included would be on the left of the graph x ≥1
Similarly, for y ≥ 2
Value of y will be unaffected by any value of x in the given equality. Also, the origin doesn’t satisfy the given inequality.
⇒ 0 ≥ 2 which is not true, hence origin is not included in the solution of the inequality.
The region to be included in the solution would be towards the left of the equality y≥ 2
The shaded region in the graph will give the answer to the required inequalities as it is the region which is covered by all the given three inequalities at the same time satisfying all the given conditions.