If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer. [Hint write an = (a – b + b)n and expand]
We can write an as
an = (a-b+b)n
We know that-
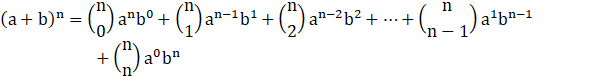
putting a = b & b = a-b, we get-
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
where ![]()
Hence (a-b) is a factor of (an-bn).
8