We know that

General term of expansion (a + b)ⁿ

We need to calculate fifth term from beginning of expansion

∴ putting r = 4, a = , and b = , we get-

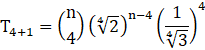
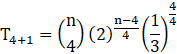
Now,

In the expression of (a + b)ⁿ

r^th term from the end = (n-r+2)^th term from the begining

Hence, 5th term from the end

= (n-5+2)^th term from the beginning

= (n-3)^th term from the beginning

Now, We need to calculate (n-3)^th term from beginning of expansion

putting r = (n-3)-1 = n-4, a = , and b = , we get-

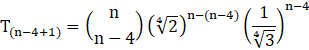
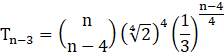
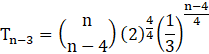
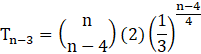
Given that-

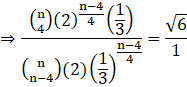
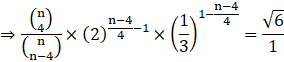
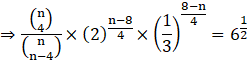
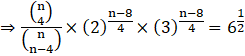
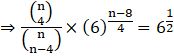
Comparing powers of 6

⇒ 2(n-8) = 4

⇒ 2n-16 = 4

⇒ 2n = 20

∴ n = 20/2 = 10

Thus, the value of n is 10.