We know that-

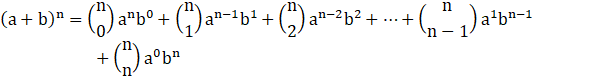
Hence

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

Thus, (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ …(1)

Putting , we get-

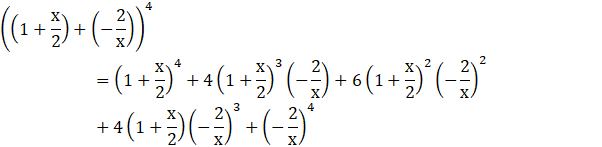
…(2)

Now Solving separately

From (1)

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

putting a = 1 & b = (x/2), we get-

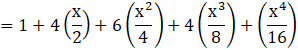
we know that-

(a + b)³ = a³ + 3a²b + 3ab² + b³

putting a = 1 & b = (x/2), we get-

Substituting the value of in (2), we get-

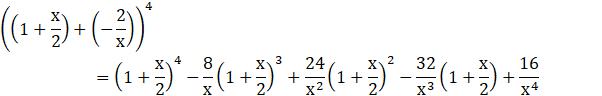
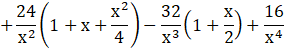
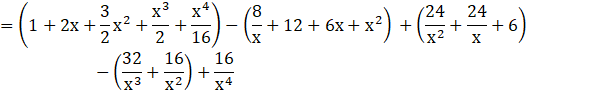
Thus,