Mathematics Part-II

Book: Mathematics Part-II

Chapter: 11. Three Dimensional Geometry

Subject: Maths - Class 12th

Q. No. 2 of Miscellaneous Exercise

Listen NCERT Audio Books - Kitabein Ab Bolengi

2

If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are (m1n2 - m2n1), (n1l2 - n2l1), (l1m2 - l2m1)

Let l, m, n be the direction cosines of the line perpendicular to each of the given lines. Then,

ll1 + mm1 + nn1 = 0 …(1)


and, ll2 + mm2 + nn2 = 0 …(2)


On solving (1) and (2) by cross - multiplication, we get -



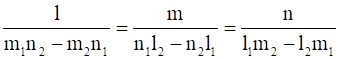
Thus, the direction cosines of the given line are proportional to


(m1n2 - m2n1), (n1l2 - n2l1), (l1m2 - l2m1)


So, its direction cosines are



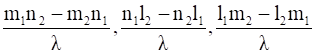
where .


we know that -


(l12 + m12 + n12) (l22 + m22 + n22) - (l1l2 + m1m2 + n1n2)2


= (m1n2 - m2n1)2 + (n1l2 - n2l1)2 + (l1m2 - l2m1)2 …(3)


It is given that the given lines are perpendicular to each other. Therefore,


l1l2 + m1m2 + n1n2 = 0


Also, we have


l12 + m12 + n12 = 1


and, l22 + m22 + n22 = 1


Putting these values in (3), we get -


(m1n2 - m2n1)2 + (n1l2 - n2l1)2 + (l1m2 - l2m1)2 = 1


⇒ λ = 1


Hence, the direction cosines of the given line are (m1n2 - m2n1), (n1l2 - n2l1), (l1m2 - l2m1)


2

Chapter Exercises

Exercise 11.1
Exercise 11.2
Exercise 11.3
Miscellaneous Exercise

More Exercise Questions

1

Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, –1), (4, 3, –1).
2

If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are (m1n2 - m2n1), (n1l2 - n2l1), (l1m2 - l2m1)
3

Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.
4

Find the equation of a line parallel to x - axis and passing through the origin.
5

If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (–4, 3, –6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
6

If the lines and are perpendicular, find the value of k.
7

Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane .
8

Find the equation of the plane passing through (a, b, c) and parallel to the plane .
9

Find the shortest distance between lines

and .
10

Find the coordinates of the point where the line through (5, 1, 6) and (3, 4,1) crosses the YZ - plane.
11

Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX - plane.
12

Find the coordinates of the point where the line through (3, –4, –5) and (2, –3, 1) crosses the plane 2x + y + z = 7.
13

Find the equation of the plane passing through the point (–1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
14

If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane , then find the value of p.
15

Find the equation of the plane passing through the line of intersection of the planes and and parallel to x-axis.
16

If O be the origin and the coordinates of P be (1, 2, –3), then find the equation of the plane passing through P and perpendicular to OP.
17

Find the equation of the plane which contains the line of intersection of the planes and . And which is perpendicular to the plane .
18

Find the distance of the point (–1, –5, –10) from the point of intersection of the line and the plane .
19

Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes s and .
20

Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:

and .
21

Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then

22

Distance between the two planes: 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is
23

The planes: 2x – y + 4z = 5 and 5x – 2.5y + 10z = 6 are