The equation of a plane passing through (x₁,y₁,z₁) is given by

A(x - x₁) + B(y - y₁) + C(z - z₁) = 0

where, A, B, C are the direction ratios of normal to the plane.

Now the plane passes through (-1,3,2)

So, equation of plane is

A(x + 1) + B(y - 3) + C(z - 2) = 0 …(1)

Since this plane is perpendicular to the given two planes.

So, their normal to the plane would be perpendicular to normals of both planes.

we know that -

is perpendicular to both &

So, required normal is cross product of normals of planes

x + 2y + 3z = 5 and 3x + 3y + z = 0

Required Normal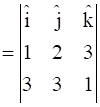

Hence, direction ratios = -7, 8, -3

∴ A = -7, B = 8, C = -3

Putting above values in (1), we get -

A(x + 1) + B(y - 3) + C(z - 2) = 0

⇒ -7(x + 1) + 8(y - 3) + (-3)(z - 2) = 0

⇒ -7x - 7 + 8y - 24 - 3z + 6 = 0

⇒ -7x + 8y - 3z - 25 = 0

∴ 7x - 8y + 3z + 25 = 0

Therefore, equation of the required plane is 7x - 8y + 3z + 25 = 0.