Find the equation of the plane passing through the line of intersection of the planes ![]() and
and ![]() and parallel to x-axis.
and parallel to x-axis.
The equation of any plane through the line of intersection of the planes ![]() and
and ![]() is given by -
is given by -
![]() .
.
So, the equation of any plane through the line of intersection of the given planes is
![]() .
.
![]() .
.
∴ ![]() . …(1)
. …(1)
Since this plane is parallel to x-axis.
So, the normal vector of the plane (1) will be perpendicular to x-axis.
Direction ratios of Normal (a1, b1, c1)≡ [(1 - 2λ), (1 - 3λ), (1 +)]
Direction ratios of x–axis (a2, b2, c2)≡ (1,0,0)
Since the two lines are perpendicular,
a1a2 + b1b2 + c1c2 = 0
(1 - 2λ) × 1 + (1 - 3λ) × 0 + (1 + λ) × 0 = 0
⇒ (1 - 2λ) = 0
∴ λ = 1/2
Putting the value of λ in (1), we get -
⇒ ![]()
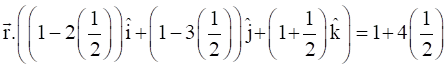
⇒ ![]()
Hence, the equation of the required plane is ![]()
15