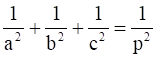
Distance of the point (x₁,y₁,z₁) from the plane Ax + By + Cz = D is

⇒

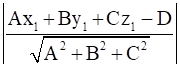
The equation of a plane having intercepts a, b, c on the x-, y-, z- axis respectively is

⇒

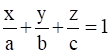
Comparing with Ax + By + Cz = D, we get -

A = 1/a, B = 1/b, C = 1/c, D = 1

Given, the plane is at a distance of 'p' units from the origin.

So, The point is O(0,0,0)

∴ x₁ = 0, y₁ = 0, z₁ = 0

Now,

Distance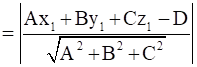

Substituting all values, we get -

⇒

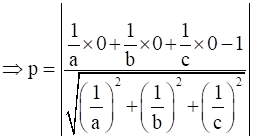
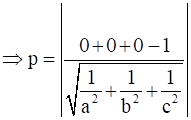
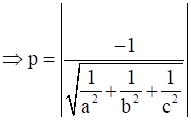
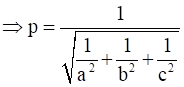
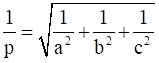
squaring both sides, we get -

⇒

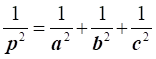
Hence Proved.