No population of any species in nature has its disposal unlimited resources to permit exponential growth. This leads to competition between individuals for limited resources. Eventually, the ‘fittest’ individual will survive and reproduce.

A population growing in a habitat with limited resources show initially a lag phase, followed by phases of acceleration and deceleration and finally an asymptote when the population density reaches the carrying capacity.

Since resources for growth for most animal populations are finite and become limiting sooner or later, the logistic growth model is considered a more realistic one.

A plot of N in relation to time (t) results in a sigmoid curve. This type of population growth is called Verhulst-Pearl Logistic Growth and is described by the following equation:

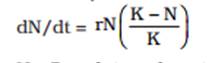
Where N = Population density at time t r = Intrinsic rate of natural increase K = Carrying capacity

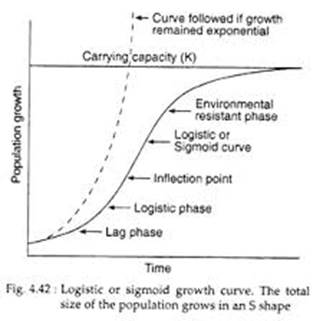
Lag phase: Initially, the population is very small because of the presence limited resource in the habitat.

Positive acceleration phase: During this phase, the organism starts adapting to its new environment and the population starts increasing. However, at the beginning of this phase, the is still limited.

Exponential phase: During this phase, the population organisms grows exponentially due to the availability of sufficient food resources, constant environment, and the absence of any interspecific competition. So, the population grows rapidly, the curve rises steeply upwards.

Negative acceleration phase: During this phase, due to increase in the environmental resistance, the growth rate of the population decreases. Increased competition among the organisms for their food and shelter is the factor responsible for the decline in the growth.

Stationary phase: During this phase, the population becomes stable. The population of the species has reached its nature’s carrying-capacity in its habitat and cannot increase any further.