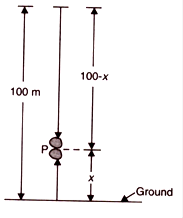
A stone is allowed to fall from the top of a tower 100 m high and at the same time another stone is projected vertically upwards from the ground with a velocity of 25 m/s. Calculate when and where the two stones will meet.
Firstly, for the stone falling from top of tower:
Height, h = (100 - x)
Initial velocity, u = 0
Time, t =?
g = 9.8 m/s2
We know that,
h = ut +![]() gt2
gt2
100 – x = 0 × t +![]() × 9.8 × t2
× 9.8 × t2
100 - x = 4.9 t2 (i)
Now, for stone projected vertically upwards:
Height, h = x
Initial velocity, u = 25 m/s
Time, t =?
g = -9.8 m/s2 (As the stone goes up)
We know that,
s = ut +![]() gt2
gt2
x = 25 × t + ![]() × (-9.8) × t2
× (-9.8) × t2
x = 25t – 4.9 t2 (ii)
Now, by adding (i) and (ii), we get:
100 – x + x = 4.9 t2 + 25 t – 4.9 t2
100 = 25 t
t = ![]()
t = 4 s
Therefore, the 2 stones will meet after a time of 4 seconds.
Now, putting the value of t in (i), we get:
100 – x = 4.9 × (4)2
100 – x = 4.9 × 16
100 – x = 78.4
100 – 78.4 = x
x = 21.6 m
Therefore, the two stones will meet at a height of 21.6 m above the ground.