Given;

f(x) = ax³ + bx – c is divisible by g(x) = x² + bx + c

Now by division Method first we have to calculate the value of ab,

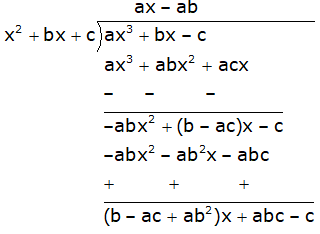
As f(x) is divisible by g(x), then remainder must be 0,

i.e.

(ab² – ac + b)x + c(ab – 1) = 0

⇒ (ab² – ac + b)x = 0 and c(ab – 1) = 0

⇒ ab² – ab + b = 0 (∵ x ≠ 0) and ab – 1 = 0 (∵ c ≠ 0)

⇒ ab – 1 = 0

⇒ ab = 1

Now take;

ab² – ac + b = 0

⇒ (ab)b – ac + b = 0

Using ab = 1 we get;

⇒ 2b – ac = 0

⇒ c = 2b/a = 2b²/ab

As ab = 1

So we get;

⇒ c = 2b²