Rocket fired from surface of mars will have kinetic energy(Positive) by virtue of speed which is taking it away from surface of mars but 20% of its initial energy is lost due to martian atmospheric resistance so its energy is less than initial energy provided to it , and gravitational potential energy(Negative) is trying to pull it towards the centre of mars , total energy of the rocket is the sum of kinetic energy remaining after atmospheric loss and gravitational potential energy , and total energy is conserved , i.e. will remain same

Now as rocket is fired upward Mars gravity will apply force on it pull it back, and speed of rocket will decrease and kinetic energy also, potential energy on other hand will increase and become less negative and at a maximum height h above the surface of mars at a distance R from centre of mars of radius r, all kinetic energy will be converted to potential energy, and rocket will come to rest and then will revert back towards surface of mars

The situation has been shown in figure

We know Kinetic Energy is given as

Where K is the kinetic energy of a body of mass moving with speed v, here we are given

Initial speed of Rocket as

v = 2 km s^–1 = 2000 ms^-1

let Mass of the rocket be m

so kinetic energy is

Now 20% of kinetic energy is lost so effective initial kinetic energy Ki is 80% of K, i.e.

= 1.6m × 10⁶ J

Now Gravitational potential energy is negative and decreases as we move away from System and at infinite distance from planet

Now Gravitational potential at a point is given by relation

U = -GMm/R

Where U is the potential Energy of a body of mass m at a point at a distance R from a centre of mass of Body of mass M, G is universal Gravitational constant

Initially Rocket is at the surface of Mars so its distance from centre of mars is equal to radius of mars i.e.

R = r = 3395 km = 3.395 × 10⁶ m

let Mass of the rocket be m

mass of planet mars is

M = 6.4 × 10²³ kg

Value of universal gravitational constant

G = 6.67 × 10^-11 Nm²Kg^-2

So putting these value we get initial potential energy U_i as

= -12.57m × 10⁶ J

Now finally after reaching a height h, the rocket will come to rest and its velocity will be 0, i.e.

v = 0 m/s

so final kinetic energy will also be zero i.e.

K_f = 0 J

Now after reaching a height h, the distance of rocket from centre of mars will be

R = r + h

So final potential energy U_f will be

i.e.

Total energy of a body is sum of kinetic energy and potential energy

T = K + U

Where T is the total energy, U is potential energy and K is kinetic energy

So total initial energy will be

T_i = U_i + K_i

i.e. T_i = -12.57 m × 10⁶ J + 1.6m × 10⁶ J

= -10.97 m × 10⁶ J

So Total Final Energy will be

T_f = U_f + K_f

i.e.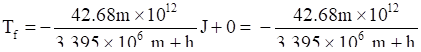

Now by law of conservation of energy we know total initial energy of rocket must be equal to total final energy of the rocket i.e.

T_i = T_f

i.e.

now cancelling out negative sign and term m from both sides and solving we get

After cross multiplication we get

37.34 × 10⁶ + 10.97h = 42.68 × 10⁶

i.e. 10.97h = 42.68 × 10⁶ - 37.34 × 10⁶ = 5.34 × 10⁶

so we get h as

h = 5.34 × 10⁶/10.97 = 0.495 × 10⁶ m

= 495 × 10³ m = 495 Km

So the rocket will reach a height of 495 Km above the surface of Mars.