Find the derivative of the following functions:
3 cot x + 5 cosec x
Let f(x) = 3 cot x + 5 cosec x
f’(x) = 3 (cot x)’ + 5 (cosec x)’
Let f1(x) = cot x, accordingly f1(x + h) = cot (x + h)
By first principle
![]()
=![]()
= ![]()
=![]()
= ![]()
= ![]()
∴ (cot x)’ = - cosec2 x ………………..(2)
Let f2(x) = cosec x, accordingly f2(x + h) = cosec (x + h)
By first principle
![]()
=![]()
=![]()
= 
= 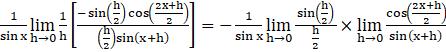
= ![]()
= -cosec x cot x
∴ (cosec x)’ = -cosec x cot x
So, f’(x) = 3 (cot x)’ + 5 (cosec x)’
Putting (cot x)’ and (cosec x)’ in f’(x)
f’(x) = 3 × (-cosec2 x) + 5 × (-cosec x cot x)
f’(x) = -3cosec2 x – 5cosec x cot x
11