It is given in the question that,

Z = 3x + 5y

We have to subject on the following equation:

x +3y ≥ 3, x+2y ≥ 2, x ≥ 0, y ≤ 0

x+y ≥ 2

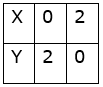
(x, y) = (0, 2), (2, 0)

x+3y ≥ 3

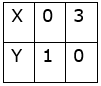
(x, y) = (0, 1), (3, 0)

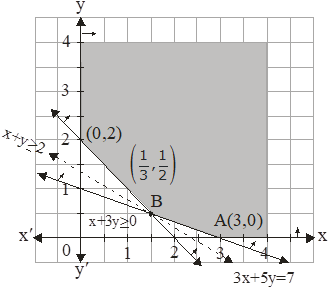
We can clearly see that the feasible region is unbounded and the corner points of the feasible region are

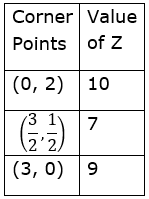
As per the table minimum value of Z is 7 but we can see that the feasible region is unbounded. Thus, 7 may or may not be the minimum value of Z

∴ We will plot the graph of inequality,

Here we will see is the resulting half plane has common points with the feasible region or not. As per the graph we can observe that the feasible region has no points in common with 3x + 5y < 7.

Hence, the minimum value of 7 is at