Minimize and Maximize Z = x + 2y subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.

Question

Philoid · Accepted Answer

It is given in the question that,

Minimize and Maximize, Z = x + 2y

We have to subject on the following equation:

X	100	0
Y	0	200

(x, y) = (100, 0), (0, 200)

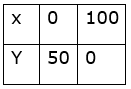
(x, y) = (0, 50), (100, 0)

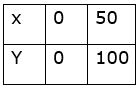
(x, y) = (0, 0), (50, 100)

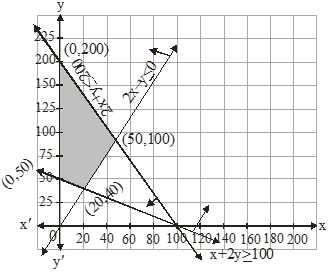
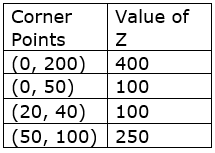
∴ It is clear that at (0, 200) Z has its maximum value i.e. 400

Also, Z is minimum at two pints (0, 50) and (20, 40)

Hence, the value of Z will be minimum at all points joining (0, 50) and (20, 40)