One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.

Question

Philoid · Accepted Answer

let there be x cakes of first kind and y cakes of second kind.

∴ x≥ 0 and y ≥ 0.

The information given in the question can be complied in given form

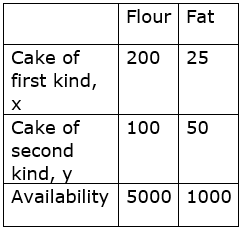
200x + 100y ≤ 5000 ⇒ 2x+ y ≤ 50

& 25x + 50y ≤ 1000 ⇒ x +2y ≤ 40

Let Z be the total number of cakes that can be made

⇒ Z =X=y

Mathematical formulation of the given problem is

Maximize Z =x+y

Subject to constraint 2x+ y ≤ 50 and x +2y ≤ 40 where x, y ≥ 0

The graphical representation shows the feasible region determined by the system of constraints.

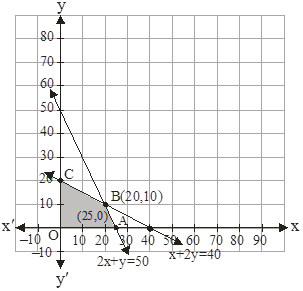
The corner points A(25, 0) , B( 20,10), 0(0,0) and C(0,20)

The values of z at these corner points are as follows

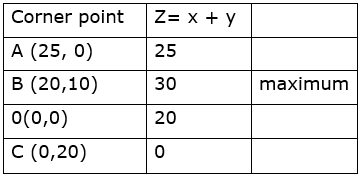
Thus, the maximum number of cakes that can be made are 30 (20 of one kind and 10 of other kind)