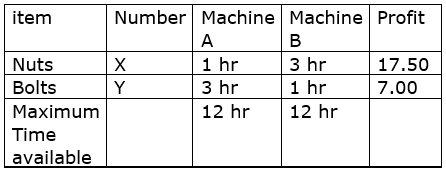
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
let the number of packages of nuts produce be x
Let the number of bolts produced be y
The tabular representation of data given is as follows:
The system of constraints is given as
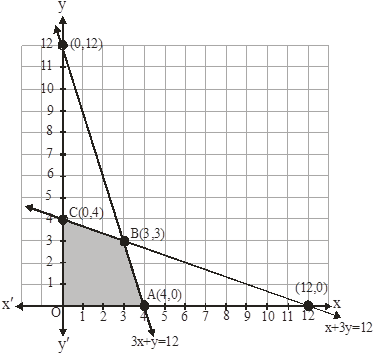
x + 3y ≤ 12
& 3y + x ≤ 12
Where x and y ≥ 0
We need to maximize the profit, so the function here will be maximizing Z
Maximize Z = 17.5x+ 7.5y
Subject to constraints
x + 3y ≤ 12
& 3y + x ≤ 12
Where x and y ≥ 0
The corner points are A(4 , 0) , B( 3,3) , C( 0 , 4) and O( 12, 0)
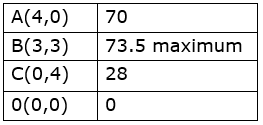
Hence the profit will be maximum if the company produces
Number of bolts – 3 packages
Number of nuts – 3 packages
Maximum profit is Rs 73.50