A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
Let the company manufacturer x souvenirs of type A and y souvenirs of type B
∴ x and y ≥ 0
The tabular representation of the given data is:
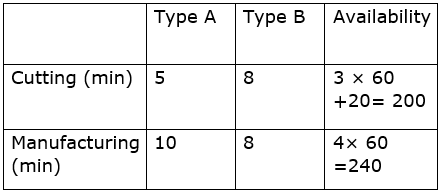
The profit on type A souvenirs is Rs 5 and that on type B souvenirs is Rs 6.
The constraints here are of the form:
5x+ 8y ≤ 200
And 10x+ 8y ≤ 240 or 5x + 4y ≤ 120
The function is to maximize the profit Z = 5x+ 6y
The mathematical formulation of the data
Maximise Z = 5x+ 6y
Subject to constraints
5x+ 8y ≤ 200
5x + 4y ≤ 120
x and y ≥ 0
The feasible region is determined by the system of constraints is as follows:
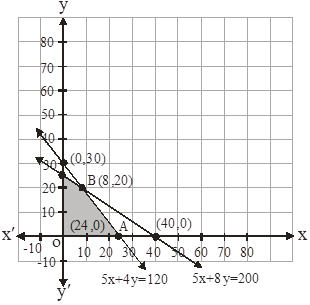
The corner points here are A( 24, 0) , B( 8, 20) and C( 0 , 25)
The value of Z at these corner points are :
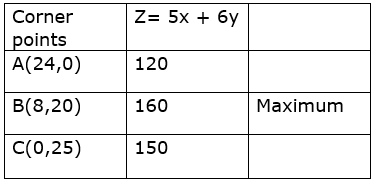
The maximum value of Z is at the point (8, 20)
Thus the firm should produce 8 number of souvenirs of type A and 20 type B souvenirs each day in order to maximize its profit of Rs160.