A merchant plans to sell two types of personal computers – a desktop model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and if his profit on the desktop model is Rs 4500 and on portable model is Rs 5000.
Let the merchant stock x number of desktop models and y number of portable models.
∴ x and y ≥ 0
According to the given condition
The cost of a desKtop model is Rs25000 and that of a portable model is Rs 40,000. The merchant can invest up to Rs 7000000
⇒ 25000x + 40000y ≤ 7000000
⇒ 5x + 8y ≤ 1400
The monthly demand of computers will not exceed 250 units.
⇒ x+ y ≤ 250
The profit on a desktop model is Rs 4500 and the profit on a portable model is Rs5000.
Total profit , Z = 4500x + 5000y
Thus the mathematical formulation of the data is
Maximize Z = 4500x + 5000y
Subject to constraints
5x + 8y ≤ 1400
x+ y ≤ 250
x and y ≥ 0
the feasible region by the system of constraints is as follows:
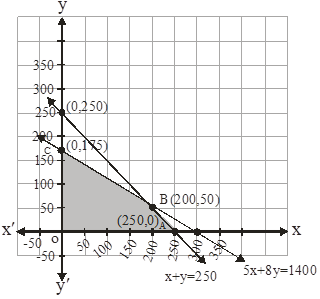
The cornet points are A(250,0) , B( 200,50) and C(0 ,175)
The value of Z at the given corners points are:
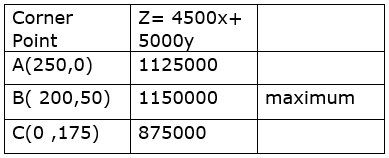
The maximum value of Z is Rs1150000 at ( 200,50)
Thus the merchant should stock 200 desktop models and 50 portable models to earn the maximum profit of Rs 11, 50, 000.