A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
let the diet contain x units of food F1 and y units of food F2.
∴ x and y ≥ 0
The tabular representation of the data is
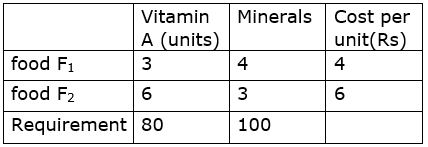
The cost of food F1 is Rs 4/unit and the cost of food F2 is Rs 6 per unit.
The constraints here are
3x + 6y ≥ 80
4x+ 3y ≥ 100
x and y ≥ 0
Total cost of the diet Z= 4x+ 6y
The mathematical formulation of the given data is
maximize Z= 4x+ 6y
Subject to constraints
3x + 6y ≥ 80
4x+ 3y ≥ 100
x and y ≥ 0
the feasible region by the system of constraints is as follows:
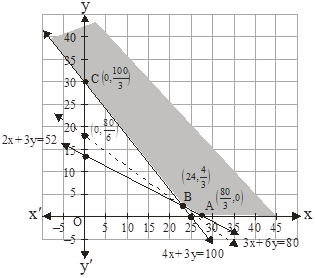
It can be seen the feasible region is unbounded with
The corner points of the feasible region are A(![]()
The values of Z at the corner points are
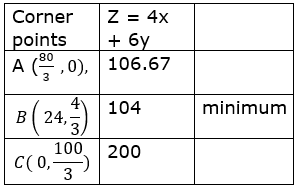
As the feasible region is unbounded therefore 104 may or may not be the minimum value of Z.
For this we will draw a graph of inequality 4x+ 6y < 104
It can be seen that the feasible region has no common points with 4x+ 6y < 104
∴ the maximum cost of the mixture will be Rs104.