There are two types of fertilisers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds that she needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs Rs 6/kg and F2 costs Rs 5/kg, determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
let the farmer buy x kf of fertilizer f1 and y kg of fertilizer f2
∴ x and y ≥ 0
The tabular representation of the data is as follows:
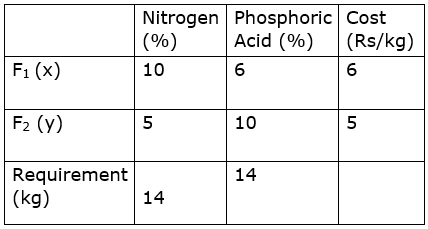
F1 consists of 10% nitrogen and F2 consists of 5% nitrogen. But the farmer requires at least 14 kg of nitrogen.
10% × x + 5% × y ≥ 14
![]()
![]() 2x+y ≥ 280
2x+y ≥ 280
food F1 consists of 6% phosphoric acid and food F2 consists of 10% phosphoric acid. But the farmer requires at least 14kg of phosphoric acid
⇒ 6% × x + 10% of y ≥ 14
⇒ ![]()
![]() 3x + 56y ≥ 700
3x + 56y ≥ 700
Total cost of fertilizers, Z= 6x+ 5y
The mathematical formulation of the given data is
Minimize, Z = 6x +5y
Subject to constraints
2x+y ≥ 280
3x + 56y ≥ 700
x and y ≥ 0
The feasible region determined by the system of constraint is:
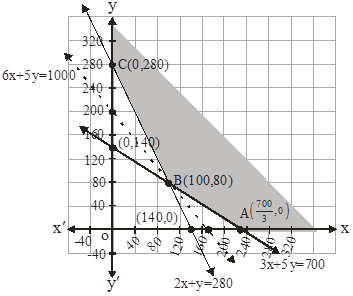
It can be seen from the graph that the feasible region is unbounded
The corner points are ![]()
The value of Z at these points are:
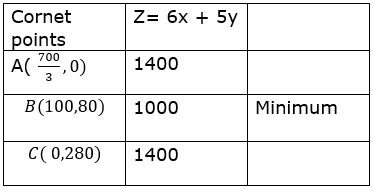
As the feasible region is unbounded, 1000 may or may not be the minimum value
For this we will draw graph of inequality
6x+ 5y < 1000
It can be seen there is no common point between feasible region and 6x+ 5y < 1000
∴ 100 KG of fertilizer F1 and 80 kg of fertilizerF2 should be used to minimize the cost and the minimum cost is Rs 1000.