The corner points of the feasible region determined by the following system of linear inequalities: 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is A. p =q B. p = 2q C. p = 3q D. q = 3p

Question

The corner points of the feasible region determined by the following system of linear inequalities: 2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is A. p =q B. p = 2q C. p = 3q D. q = 3p

Philoid · Accepted Answer

In the given question the constraints are

2x + y ≤ 10,

x + 3y ≤ 15,

and x, y ≥ 0

The function is to maximize Z = px + qy

The corner points are (0, 0), (5, 0), (3, 4) and (0, 5).

The value of Z at these points are

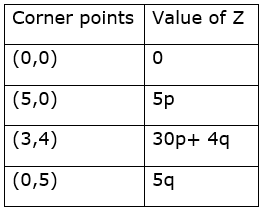
Since the maximum value of z occurs on (3, 4) and (0, 5)

Hence the value on (3, 4) = Value on (0, 5)

3p+ 4q = 5q

3p = q

∴ Value of Z will be maximum if q =3p

Hence D is the correct answer.