let x and y be the number of packets of food P and Q respectively. Obviously, x ≥ 0, y ≥ 0. Mathematical formulation of given problem is as follows:

Maximize Z = 6x + 3y ….(1)

Subject to the constraints,

12x + 3y ≥ 240 (constraint on calcium) i.e. 4x + y ≥ 80 …..(2)

4x + 20y ≥ 460 (constraint on iron) i.e. x + 5y ≥ 115 …..(3)

6x + 4y ≤ 300 (constraint on cholesterol) i.e. 3x + 2y ≤ 150 ….(4)

x ≥ 0, y ≥ 0 ….(5)

Now let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is bounded.

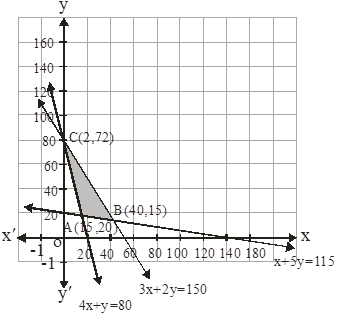
The coordinates of the corner points A(15,20),B(40,15), and C(2,72).

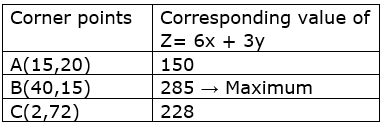
Now, we find the maximum value of Z. According to table the maximum value of Z = 285 at point B (40,15).

Hence, to get the maximum amount of vitamin A in the diet, the packets of food P should be 40 and the packets of food Q should be 15. The maximum amount of vitamin A will be 285.