A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
let x and y be the amount of two bands P and Q respectively which are mixed. Obviously, x ≥ 0, y ≥ 0.
The given information can be formulated in a table as:
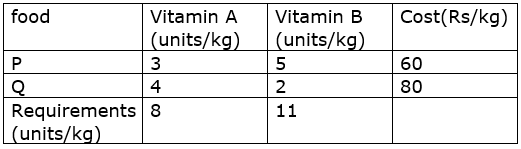
Mathematical formulation of given problem is as follows:
Maximize Z = 250x + 200y ….(1)
Subject to the constraints,
3x + 1.5y ≥ 18 …..(2)
2.5x + 11.25y ≥ 45 …..(3)
2x + 3y ≥ 24 ….(4)
x ≥ 0, y ≥ 0 ….(5)
Now let us graph the feasible region of the system of inequalities (2) to (5).
The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is unbounded.
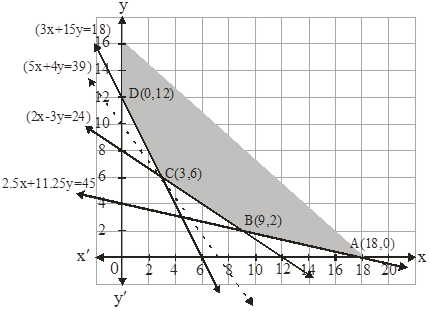
The coordinates of the corner points A(18,0), B(9,2), C(3,6) and D(0,12).

As, feasible region is unbounded so 1950 may or may not be minimum value of Z.
So, 1950 is the minimum value of Z, if the open half plane is determined by 250x + 200y <1950 has no point in common with the feasible region. Otherwise z has no minimum value.
For this we will draw the graph of inequality 250x + 200y <1950 or 5x + 4y < 39. Here we find that 250x + 200y <1950 has no point in common with the feasible region. Hence the minimum value of Z is 1950 at C(3,6).
So, 3 and 6 be the amount of two bands P and Q respectively which are mixed to get minimum cost to Rs 1950.