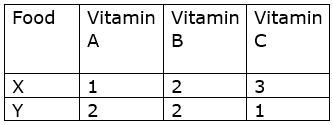
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below: One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?

Question

Philoid · Accepted Answer

let x kg and y kg be amount of food X and Y respectively. Obviously x ≥ 0, y ≥ 0. Mathematical formulation of given problem is as follows:

Minimize Z = 16x + 20y ….(1)

Subject to the constraints,

x + 2y ≥ 10 …..(2)

x + y ≥ 6 …..(3)

3x + y ≥ 8 ….(4)

x ≥ 0, y ≥ 0 ….(5)

Now let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is unbounded.

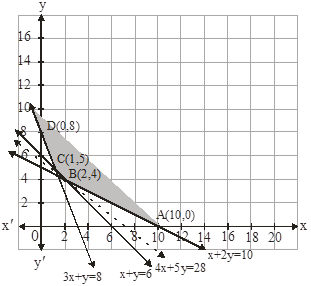
The coordinates of the corner points A(10,0),B(2,4), C(1,5)and D(0,8).

As, feasible region is unbounded so 112 may or may not be minimum value of Z.

So, 112 is the minimum value of Z, if the open half plane is determined by 16x + 20y <112 has no point in common with the feasible region. Otherwise z has no minimum value.

For this we will draw the graph of inequality 16x + 20y <112 or 4x + 5y<28. Here we find that 16x + 20y <112 has no point in common with the feasible region. Hence the minimum value of Z is 112 at B(2,4).

So, 2kg and 4kg be the amount of two foods P and Q respectively which are mixed to get minimum cost to Rs 112.