A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
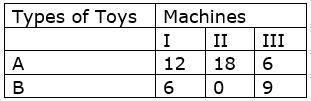
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
let x and y be the number of toys manufactured per day of type A and B respectively. Obviously x ≥ 0, y ≥ 0. Mathematical formulation of given problem is as follows:
Maximize Z = 7.5x + 5y ….(1)
Subject to the constraints,
2x + y ≤ 60 …..(2)
x ≤ 60 …..(3)
2x + 3y ≤ 120 ….(4)
x ≥ 0, y ≥ 0 ….(5)
Now let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is bounded.
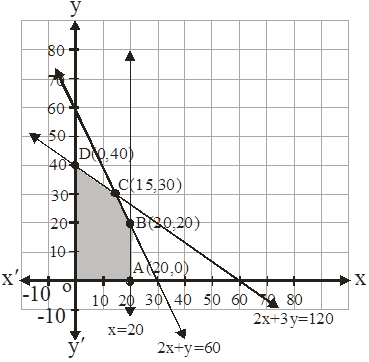
The coordinates of the corner points A(20,0),B(20,20), C(15,30)and D(0,40).

Now, we find the maximum value of Z. According to table the maximum value of Z = 262.5 at point C (15,30).
Hence, 15 and 20 be the number of toys manufactured per day of type A and B respectively to get the maximum profit.