An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
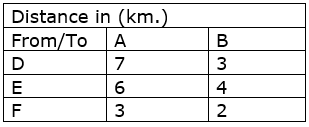
Assuming that the transportation cost of 10 liters of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?
let x and y liters of oil be supplied by A to shop D and E respectively. Then 7000 - x - y will be supplied to F. Obviously x ≥ 0, y ≥ 0.
Since requirement at D is 4500L but supplied x quintal hence, 4500 - x is sent form B to D.
Similarly requirement at E is 3000L but supplied y quintal hence, 3000 - y is sent form B to E.
Similarly requirement at E is 3500 quintal but supplied 7000 - x - y quintal hence, 3500 - (7000 - x - y) i.e. x + y - 3500 is sent form B to E.
Diagrammatically it can be explained as:
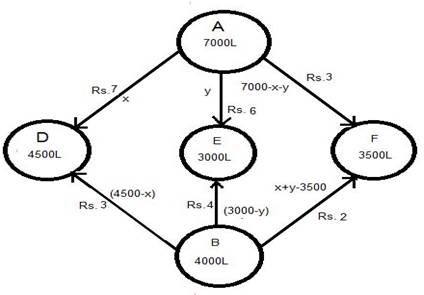
As x ≥ 0, y ≥ 0 and 7000 - x - y ≥ 0 ⇒ x + y ≤ 7000
4500 - x ≥ 0, 3000 - y ≥ 0 and x + y - 3500 ≥ 0
⇒ x ≤ 4500, y ≤ 3000 and x + y ≥ 3500
Cost of delivering 10L of petrol = Re.1
Then Cost of delivering 1L of petrol = Rs.1/10
Total transportation cost Z can be calculated as:
Z = 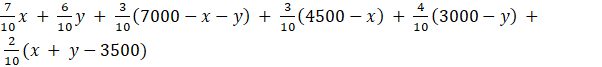
Z = 0.3x + 0.1y + 3950
Mathematical formulation of given problem is as follows:
Minimize Z = 0.3x + 0.1y + 3950 ….(1)
Subject to the constraints,
x + y ≤ 7000 …..(2)
x ≤ 4500 …..(3)
y ≤ 3000 ….(4)
x + y ≥ 3500 …(5)
x ≥ 0, y ≥ 0 ….(6)
Now let us graph the feasible region of the system of inequalities (2) to (6). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is bounded.
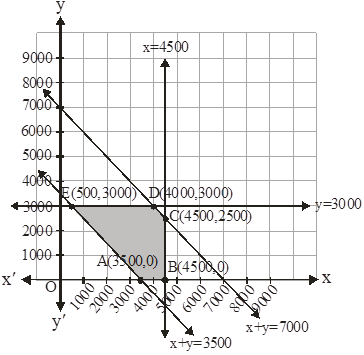
The coordinates of the corner points A(3500,0),B(4500,0),C(4500,2500), D(4000,3000) and E(500,3000) .

Now, we find the minimum value of Z. According to table the minimum value of Z = 4400 at point E (500,3000).
Hence, the amount of oil delivered from A to D, E and F is 500L, 3000L and 3500L quintals respectively and from B to D,E and F is 4000L, 0 L and 0 L respectively.