A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
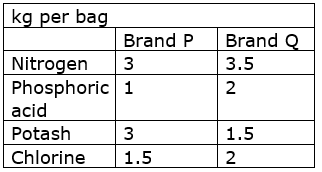
let x and y be the bags of brands P and Q respectively. Obviously x ≥ 0, y ≥ 0. Mathematical formulation of given problem is as follows:
Minimize Z = 3x + 3.5y ….(1)
Subject to the constraints,
x + 2y ≤ 240 …..(2)
3x + 1.5y ≤ 270 ⇒ x + 0.5y=90 …..(3)
1.5x + 2y ≤ 310 ….(4)
x ≥ 0, y ≥ 0 ….(5)
Now let us graph the feasible region of the system of inequalities (2) to (5). The feasible region (shaded) is shown in the fig. Here, we can observe that the feasible region is bounded.
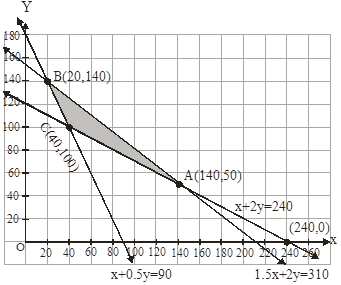
The coordinates of the corner points A(140,50),B(20,40) and C(40,100).

Now, we find the minimum value of Z. According to table the minimum value of Z = 470 at point C (40,100).
Hence, 40 and 100 be be the bags of brands P and Q respectively to be added to the garden to minimize the amount of nitrogen.